Implied volatility isn’t flat across strikes: it curves. It’s like a smile: the volatility smile.
When plotted against strike price, implied volatilities for call options typically form a smile, with lower volatilities near-the-money and higher volatilities deep in- or out-of-the-money. This shape reflects real-world market dynamics, like the increased demand for tail-risk protection and limitations of the Black-Scholes model.
In this article, we’ll implement a simple C++ tool to compute this volatility smile from observed market prices, helping us visualize and understand its structure.
1. What’s a Volatility Smile?
A volatility smile is a pattern observed in options markets where implied volatility (IV) is not constant across different strike prices — contrary to what the Black-Scholes model assumes. When plotted (strike on the x-axis, IV on the y-axis), the graph forms a smile-shaped curve.
- At-the-money (ATM) options tend to have the lowest implied volatility.
- In-the-money (ITM) and out-of-the-money (OTM) options show higher implied volatility.
If you plot IV vs. strike price, the shape curves upward at both ends, resembling a smile.
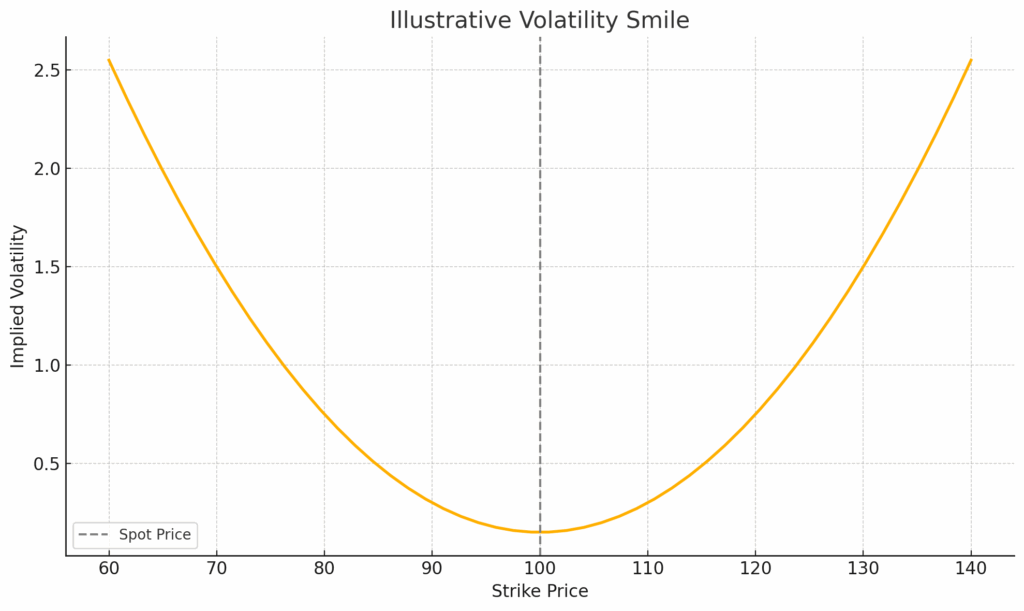
Implied volatility is lowest near the at-the-money (ATM) strike and increases for both in-the-money (ITM) and out-of-the-money (OTM) options.
This convex shape reflects typical market observations and diverges from the flat IV assumption in Black-Scholes.
For call options, the left side of the volatility smile (low strikes) is in-the-money, the center is at-the-money, and the right side (high strikes) is out-of-the-money.
2. In-the-money (ITM), At-the-money (ATM), Out-of-the-money (OTM)
These terms describe the moneyness of an option:
| Option Type | In-the-money (ITM) | At-the-money (ATM) | Out-of-the-money (OTM) |
|---|---|---|---|
| Call | Strike < Spot | Strike ≈ Spot | Strike > Spot |
| Put | Strike > Spot | Strike ≈ Spot | Strike < Spot |
- ITM: Has intrinsic value — profitable if exercised now.
- ATM: Strike is close to spot price — most sensitive to volatility (highest gamma).
- OTM: No intrinsic value — only time value.
Here are two quick scenarios:
In-the-Money (ITM) Call – Profitable Scenario:
A trader buys a call option with a strike price of £90 when the stock is at £95 (already ITM).
Later, the stock rises to £105, and the option gains intrinsic value.
🔁 Trader profits by exercising the option or selling it for more than they paid.
Out-of-the-Money (OTM) Call – Profitable Scenario:
A trader buys a call option with a strike price of £110 when the stock is at £100 (OTM, cheaper).
Later, the stock jumps to £120, making the option now worth at least £10 intrinsic.
🔁 Trader profits from the big move, even though the option started OTM.
3. Why this pattern?
The volatility smile arises because market participants do not believe asset returns follow a perfect normal distribution. Instead, they expect more frequent extreme moves in either direction, what statisticians call “fat tails.” To account for this, traders are willing to pay more for options that are far out-of-the-money or deep in-the-money, especially since these positions offer outsized payoffs in rare but impactful events. This increased demand pushes up the implied volatility for these strikes.
Moreover, options at the tails often serve as hedging tools.
- For example, portfolio managers commonly buy far out-of-the-money puts to protect against a market crash. Similarly, speculative traders might buy cheap out-of-the-money calls hoping for a large upward movement. This consistent demand at the tails drives up their prices, and consequently, their implied volatilities.
- In contrast, at-the-money options are more frequently traded and are typically the most liquid. Because their strike price is close to the current market price, they tend to reflect the market’s consensus on future volatility more accurately. There’s less uncertainty and speculation around them, and they don’t carry the same kind of tail risk premium.
As a result, the implied volatility at the money tends to be lower, forming the bottom of the volatility smile.
4. Implementation in C++
Here is an implementation in C++ using Black-Scholes:
#include <iostream>
#include <cmath>
#include <vector>
#include <iomanip>
// Black-Scholes formula for a European call option
double black_scholes_call(double S, double K, double T, double r, double sigma) {
double d1 = (std::log(S / K) + (r + 0.5 * sigma * sigma) * T) / (sigma * std::sqrt(T));
double d2 = d1 - sigma * std::sqrt(T);
auto N = [](double x) {
return 0.5 * std::erfc(-x / std::sqrt(2));
};
return S * N(d1) - K * std::exp(-r * T) * N(d2);
}
// Bisection method to compute implied volatility
double implied_volatility(double market_price, double S, double K, double T, double r,
double tol = 1e-5, int max_iter = 100) {
double low = 0.0001;
double high = 2.0;
for (int i = 0; i < max_iter; ++i) {
double mid = (low + high) / 2.0;
double price = black_scholes_call(S, K, T, r, mid);
if (std::abs(price - market_price) < tol) return mid;
if (price > market_price) high = mid;
else low = mid;
}
return (low + high) / 2.0; // best guess
}
// Synthetic volatility smile to simulate market prices
double synthetic_volatility(double K, double S) {
double base_vol = 0.15;
return base_vol + 0.0015 * std::pow(K - S, 2);
}
int main() {
double S = 100.0; // Spot price
double T = 0.5; // Time to maturity in years
double r = 0.01; // Risk-free rate
std::cout << "Strike\tMarketPrice\tImpliedVol\n";
for (double K = 60; K <= 140; K += 2.0) {
double true_vol = synthetic_volatility(K, S);
double market_price = black_scholes_call(S, K, T, r, true_vol);
double iv = implied_volatility(market_price, S, K, T, r);
std::cout << std::fixed << std::setprecision(2)
<< K << "\t" << market_price << "\t\t" << std::setprecision(4) << iv << "\n";
}
return 0;
}We aim to simulate and visualize a volatility smile by:
- Generating synthetic market prices for European call options using a non-constant volatility function.
- Computing the implied volatility by inverting the Black-Scholes model using a bisection method.
- Printing the results to observe how implied volatility varies across strike prices.
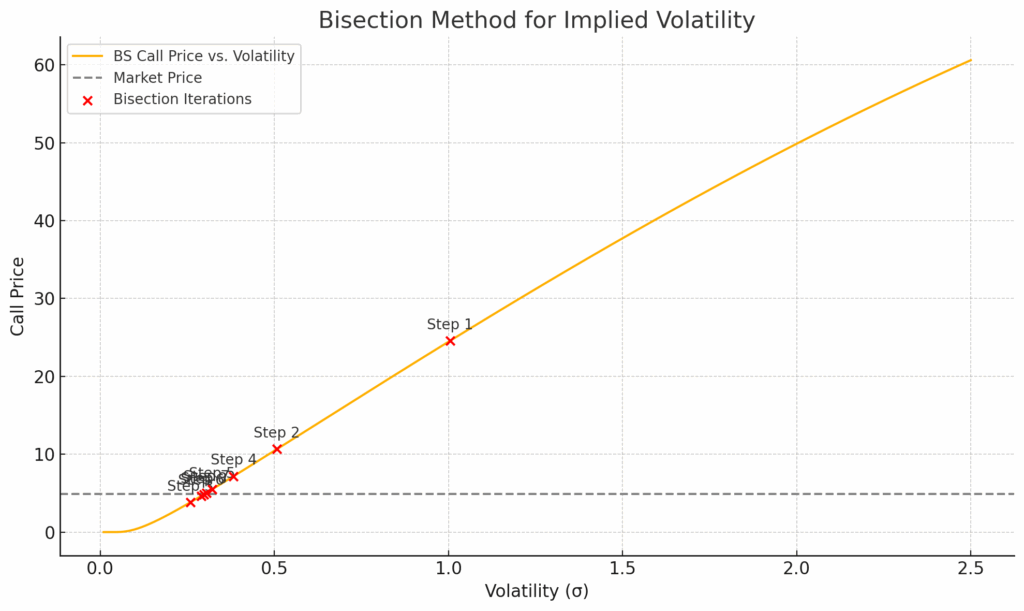
We compute implied volatility by numerically inverting the Black-Scholes formula:
double implied_volatility(double market_price, double S, double K, double T, double r)
We seek the value of [math]\sigma[/math] such that:
[math] C_{\text{BS}}(S, K, T, r, \sigma) \approx \text{Market Price} [/math]
We use the bisection method, iteratively narrowing the interval [math][\sigma_{\text{low}}, \sigma_{\text{high}}][/math] until the difference between the model price and the market price is within a small tolerance.
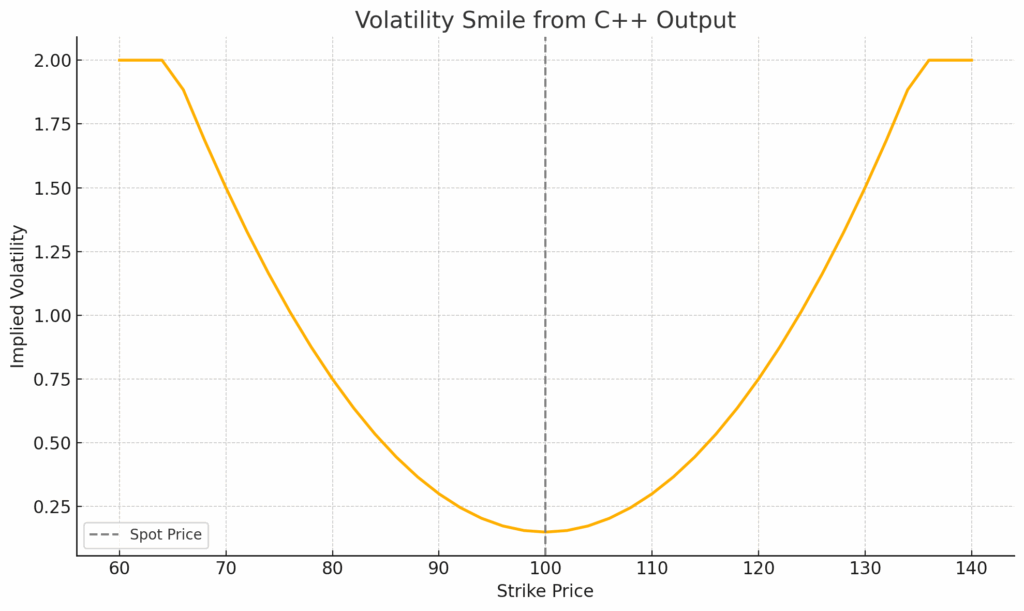
Now, here is the plot of your volatility smile using the output from the C++ program.
After compiling our code:
mkdir build
cd build
cmake ..
makeWe can run it:
./volatilitysmileAnd get:
Strike MarketPrice ImpliedVol
60.00 72.18 2.0000
62.00 68.21 2.0000
64.00 64.09 2.0000
66.00 59.85 1.8840
68.00 55.55 1.6860
70.00 51.23 1.5000
72.00 46.92 1.3260
74.00 42.68 1.1640
76.00 38.53 1.0140
78.00 34.51 0.8760
80.00 30.64 0.7500
82.00 26.95 0.6360
84.00 23.45 0.5340
86.00 20.17 0.4440
88.00 17.11 0.3660
90.00 14.28 0.3000
92.00 11.70 0.2460
94.00 9.38 0.2040
96.00 7.36 0.1740
98.00 5.70 0.1560
100.00 4.47 0.1500
102.00 3.73 0.1560
104.00 3.44 0.1740
106.00 3.57 0.2040
108.00 4.06 0.2460
110.00 4.91 0.3000
112.00 6.10 0.3660
114.00 7.64 0.4440
116.00 9.55 0.5340
118.00 11.83 0.6360
120.00 14.48 0.7500
122.00 17.49 0.8760
124.00 20.86 1.0140
126.00 24.57 1.1640
128.00 28.59 1.3260
130.00 32.89 1.5000
132.00 37.44 1.6860
134.00 42.19 1.8840
136.00 47.07 2.0000
138.00 52.03 2.0000
140.00 57.01 2.0000As expected, implied volatility is lowest near the at-the-money strike (100) and rises symmetrically for deep in-the-money and out-of-the-money strikes forming the characteristic smile shape:
The code for this article is accessible here:
https://github.com/cppforquants/volatilitysmile