Futures

Futures contracts derive their value from the underlying asset, but their price is not always equal to the spot price. The cost-of-carry model explains this difference by accounting for interest rates, storage costs, and dividends. It’s a fundamental concept in pricing futures and understanding arbitrage relationships. In this article, we’ll break down the formula and implement a clean, flexible version in C++. Whether you’re pricing equity, commodity, or FX futures, this model offers a solid foundation. How to calculate the cost-of-carry in C++?

1. What’s a Future?

A future is a standardized financial contract that obligates the buyer to purchase, or the seller to sell, an underlying asset at a predetermined price on a specified future date.

Unlike forwards, futures are traded on exchanges and are marked to market daily, meaning gains and losses are settled each day until the contract expires. They are commonly used for hedging or speculation across a wide range of assets, including commodities, equities, interest rates, and currencies.

Futures contracts help investors manage risk by locking in prices, and they also play a key role in price discovery in global markets.

2. The Cost-of-Carry Formula

The cost-of-carry model provides a theoretical price for a futures contract based on the current spot price of the asset and the costs (or benefits) of holding the asset until the contract’s expiration. These costs include financing (via interest rates), storage (for physical goods), and dividends or income lost by holding the asset instead of investing it elsewhere.

The formula is:

[math] \Large F_t = S_t \cdot e^{(r + u – q)(T – t)} [/math]

Where:

• [math] F_t [/math]: Theoretical futures price at time [math] t [/math]
• [math] S_t [/math]: Spot price of the underlying asset
• [math] r [/math]: Risk-free interest rate (annualized)
• [math] u [/math]: Storage cost (as a percentage, annualized)
• [math] q [/math]: Dividend yield or convenience yield (annualized)
• [math] T – t [/math]: Time to maturity in years

This formula assumes continuous compounding. In practice:

• For equity index futures, [math] u = 0 [/math], but [math] q > 0 [/math]
• For commodities like oil or gold, [math] u > 0 [/math], and [math] q = 0 [/math]
• For FX futures, [math] r [/math] and [math] q [/math] represent the interest rate differential between two currencies

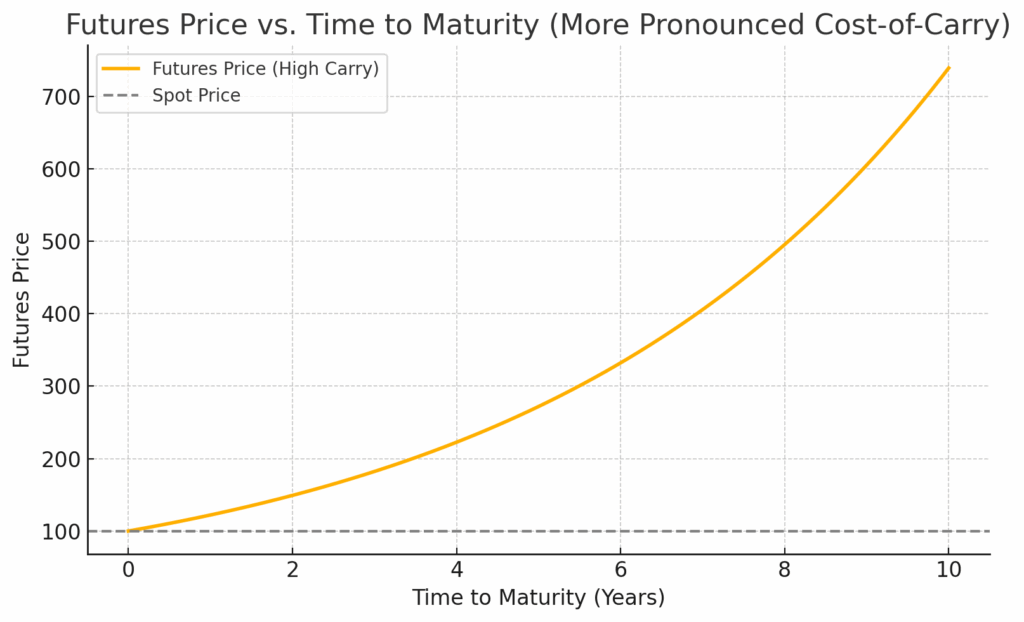
The cost-of-carry explains why futures can trade at a premium or discount to the spot price, depending on these inputs.

An example of this cost, when the spot price stays the same:

Now how to calculate the cost-of-carry in C++?

3. A Flexible C++ Implementation

Below is a self-contained example that takes spot price, interest rate, storage cost, dividend yield, and time to maturity as inputs and outputs the futures price.

Here’s a complete, ready-to-run C++ program:

#include <iostream>
#include <cmath>

struct FuturesPricingInput {
    double spot_price;
    double risk_free_rate;
    double storage_cost;
    double dividend_yield;
    double time_to_maturity; // in years
};

double price_futures(const FuturesPricingInput& input) {
    double exponent = (input.risk_free_rate + input.storage_cost - input.dividend_yield) * input.time_to_maturity;
    return input.spot_price * std::exp(exponent);
}

int main() {
    FuturesPricingInput input {
        100.0,   // spot_price
        0.05,    // risk_free_rate (5%)
        0.01,    // storage_cost (1%)
        0.02,    // dividend_yield (2%)
        0.5      // time_to_maturity (6 months)
    };

    double futures_price = price_futures(input);
    std::cout << "Futures price: " << futures_price << std::endl;

    return 0;
}

Let’s write that code in a futures.cpp file, create a CMakeLists.txt:

cmake_minimum_required(VERSION 3.10)
project(futures)
set(CMAKE_CXX_STANDARD 17)
add_executable(futures ../futures.cpp)

And compile it:

mkdir build 
cd build
cmake ..
make

The result is the price of our future:

➜  build ./futures 
Futures price: 102.02