Maintaining consistent C++ style across a large codebase is one of the simplest ways to improve readability, reduce onboarding time, and prevent unnecessary merge conflicts. Yet many C++ teams, especially in quantitative finance, where codebases grow organically over years still rely on manual style conventions or developer-specific habits. The result is familiar: inconsistent indentation, mixed brace styles, scattered spacing rules, and code that “looks” different depending on who touched it last. Clang-Format solves this problem. What is Clang formatting for C++?
Part of the Clang and LLVM ecosystem, clang-format is a fast, deterministic, fully automated C++ formatter that rewrites your source code according to a predefined set of style rules. Instead of arguing about formatting in code reviews or spending time manually cleaning up diffs, quant developers can enforce a single standard across an entire pricing or risk library automatically and reproducibly.
1.What is the Clang and LLVM ecosystem?
The Clang and LLVM ecosystem is a modern, modular compiler toolchain used for building, analyzing, and optimizing C++ (and other language) programs. Clang is the front-end: it parses C++ code, checks syntax and types, produces highly readable diagnostics, and generates LLVM’s intermediate representation (IR). LLVM is the backend: a collection of reusable compiler components that optimize the IR and generate machine code for many architectures (x86-64, ARM, etc.). Unlike monolithic compilers like GCC, the Clang/LLVM stack is built as independent libraries, which makes it incredibly flexible.
This design allows developers to build tools such as clang-format, clang-tidy, source-to-source refactoring engines, static analyzers, and custom compiler plugins. The ecosystem powers modern IDE features, code intelligence, and even JIT-compiled systems.
Because of its modularity, fast compilation, modern C++ standard support, and rich tooling, Clang/LLVM has become the backbone of many large C++ codebases, including those used in finance, gaming, scientific computing, and operating systems like macOS.
2.Clang-Format: The Modern Standard for C++ Code Formatting
Clang-format has become the default choice for formatting C++ code across many industries, from finance to large-scale open-source projects. Built on top of the Clang and LLVM ecosystem, it provides a fast, deterministic, and fully automated way to enforce consistent style rules across an entire codebase.
Instead of relying on ad-hoc conventions or individual preferences, teams can define a single .clang-format configuration and apply it uniformly through editors, CI pipelines, and pre-commit hooks. The result is cleaner diffs, fewer formatting discussions in code reviews, and a more maintainable codebase—crucial benefits for large C++ systems such as pricing engines, risk libraries, or high-performance trading infrastructure.
3.Installation
How to start using Clang formatting for C++? Let’s start with installation.
I’m using mac, and it’s as simple as:
➜ ~ brew install clang-format
==> Fetching downloads for: clang-format
✔︎ Bottle Manifest clang-format (21.1.6) [Downloaded 12.7KB/ 12.7KB]
✔︎ Bottle clang-format (21.1.6) [Downloaded 1.4MB/ 1.4MB]
==> Pouring clang-format--21.1.6.sonoma.bottle.tar.gz
🍺 /usr/local/Cellar/clang-format/21.1.6: 11 files, 3.4MB
==> Running `brew cleanup clang-format`...With linux, it would also be as simple as:
➜ ~ sudo apt-get install clang-formatTo get a general overview of the tool, just run the –help command:
➜ ~ clang-format --help
OVERVIEW: A tool to format C/C++/Java/JavaScript/JSON/Objective-C/Protobuf/C# code.
If no arguments are specified, it formats the code from standard input
and writes the result to the standard output.
If <file>s are given, it reformats the files. If -i is specified
together with <file>s, the files are edited in-place. Otherwise, the
result is written to the standard output.
USAGE: clang-format [options] [@<file>] [<file> ...]
OPTIONS:
Clang-format options:
--Werror - If set, changes formatting warnings to errors
--Wno-error=<value> - If set, don't error out on the specified warning type.
=unknown - If set, unknown format options are only warned about.
This can be used to enable formatting, even if the
configuration contains unknown (newer) options.
Use with caution, as this might lead to dramatically
differing format depending on an option being
supported or not.
--assume-filename=<string> - Set filename used to determine the language and to find
.clang-format file.
Only used when reading from stdin.
If this is not passed, the .clang-format file is searched
relative to the current working directory when reading stdin.
Unrecognized filenames are treated as C++.
supported:
CSharp: .cs
Java: .java
JavaScript: .js .mjs .cjs .ts
Json: .json .ipynb
Objective-C: .m .mm
Proto: .proto .protodevel
TableGen: .td
TextProto: .txtpb .textpb .pb.txt .textproto .asciipb
Verilog: .sv .svh .v .vh
--cursor=<uint> - The position of the cursor when invoking
clang-format from an editor integration
--dry-run - If set, do not actually make the formatting changes
--dump-config - Dump configuration options to stdout and exit.
Can be used with -style option.
--fail-on-incomplete-format - If set, fail with exit code 1 on incomplete format.
--fallback-style=<string> - The name of the predefined style used as a
fallback in case clang-format is invoked with
-style=file, but can not find the .clang-format
file to use. Defaults to 'LLVM'.
Use -fallback-style=none to skip formatting.
--ferror-limit=<uint> - Set the maximum number of clang-format errors to emit
before stopping (0 = no limit).
Used only with --dry-run or -n
--files=<filename> - A file containing a list of files to process, one per line.
-i - Inplace edit <file>s, if specified.
--length=<uint> - Format a range of this length (in bytes).
Multiple ranges can be formatted by specifying
several -offset and -length pairs.
When only a single -offset is specified without
-length, clang-format will format up to the end
of the file.
Can only be used with one input file.
--lines=<string> - <start line>:<end line> - format a range of
lines (both 1-based).
Multiple ranges can be formatted by specifying
several -lines arguments.
Can't be used with -offset and -length.
Can only be used with one input file.
-n - Alias for --dry-run
--offset=<uint> - Format a range starting at this byte offset.
Multiple ranges can be formatted by specifying
several -offset and -length pairs.
Can only be used with one input file.
--output-replacements-xml - Output replacements as XML.
--qualifier-alignment=<string> - If set, overrides the qualifier alignment style
determined by the QualifierAlignment style flag
--sort-includes - If set, overrides the include sorting behavior
determined by the SortIncludes style flag
--style=<string> - Set coding style. <string> can be:
1. A preset: LLVM, GNU, Google, Chromium, Microsoft,
Mozilla, WebKit.
2. 'file' to load style configuration from a
.clang-format file in one of the parent directories
of the source file (for stdin, see --assume-filename).
If no .clang-format file is found, falls back to
--fallback-style.
--style=file is the default.
3. 'file:<format_file_path>' to explicitly specify
the configuration file.
4. "{key: value, ...}" to set specific parameters, e.g.:
--style="{BasedOnStyle: llvm, IndentWidth: 8}"
--verbose - If set, shows the list of processed files
Generic Options:
--help - Display available options (--help-hidden for more)
--help-list - Display list of available options (--help-list-hidden for more)
--version - Display the version of this program4.Usage
Imagine a messy piece of C++ code calculating DVA with formatting problems all over:
#include <iostream>
#include<vector>
#include <cmath>
double computeDVA(const std::vector<double>& exposure,
const std::vector<double>& pd,
const std::vector<double> lgd, double discount)
{
double dva=0.0;
for (size_t i=0;i<exposure.size();i++){
double term= exposure[i] * pd[i] * lgd[i] *discount;
dva+=term;
}
return dva; }
int main() {
std::vector<double> exposure = {100,200,150,120};
std::vector<double> pd={0.01,0.015,0.02,0.03};
std::vector<double> lgd = {0.6,0.6,0.6,0.6};
double discount =0.97;
double dva = computeDVA(exposure,pd,lgd,discount);
std::cout<<"DVA: "<<dva<<std::endl;
return 0;}
This respects the general DVA formula (from the XVA family):

Let’s format it with clang-format using the LLVM style, I run:
clang-format -i -style=LLVM dva.cppwith:
-i = overwrite the file in place
-style=LLVM = apply the LLVM formatting style
It becomes sweet and nice:
#include <cmath>
#include <iostream>
#include <vector>
double computeDVA(const std::vector<double> &exposure,
const std::vector<double> &pd, const std::vector<double> lgd,
double discount) {
double dva = 0.0;
for (size_t i = 0; i < exposure.size(); i++) {
double term = exposure[i] * pd[i] * lgd[i] * discount;
dva += term;
}
return dva;
}
int main() {
std::vector<double> exposure = {100, 200, 150, 120};
std::vector<double> pd = {0.01, 0.015, 0.02, 0.03};
std::vector<double> lgd = {0.6, 0.6, 0.6, 0.6};
double discount = 0.97;
double dva = computeDVA(exposure, pd, lgd, discount);
std::cout << "DVA: " << dva << std::endl;
return 0;
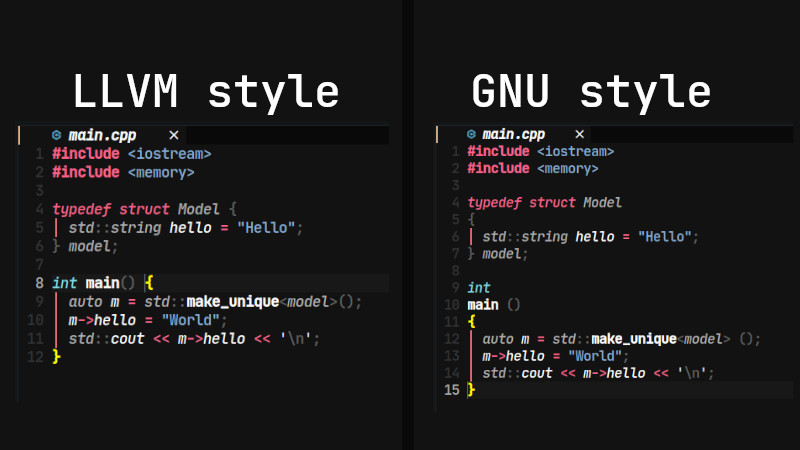
}5. A List and Comparison of The Clang Styles
Formatting styles in clang-format come from real, large-scale C++ codebases: LLVM, Google, Chromium, Mozilla, and others. Each style reflects the conventions of the organization that created it, and each emphasizes different priorities such as readability, compactness, or strict consistency. While clang-format supports many styles, they all serve the same purpose: enforcing a predictable, automated layout for C++ code across complex projects. Here is an overview of Clang formatting for C++ via a list of styles available:
| Style | Origin / Used By | Brace Style | Indentation | Line Length | Notable Traits |
|---|---|---|---|---|---|
| LLVM | LLVM/Clang project | Stroustrup-like | 2 spaces | 80 | Clean, minimal, modern; default for clang-format |
| Google C++ Style Guide | Allman/Google | 2 spaces | 80 | Very consistent; strong whitespace rules | |
| Chromium | Chromium/Google Chrome | K&R | 2 spaces | 80 | Optimized for very large codebases |
| Mozilla | Firefox | Allman | 2 or 4 spaces | 99 | Slightly looser than Google; readable |
| WebKit | WebKit / Safari | Stroustrup | 4 spaces | 120 | Widely spaced; readable for UI and engine code |
| GNU | GNU coding standard | GNU style | 2 spaces | 79 | Uncommon now; unusual brace placements |
| Microsoft | Microsoft C++/C# | Allman | 4 spaces | 120 | Familiar to Windows devs; wide spacing |
| JS | JavaScript projects | K&R | 2 spaces | 80 | For JS/TS/CSS formatting, not C++ |
| File | Custom .clang-format | — | — | — | User-defined rules; highly flexible |
Among all available clang-format styles, LLVM stands closest to a true industry standard for modern C++ development. Its clean, neutral layout makes it easy to read, easy to maintain, and suitable for teams of any size: from open-source contributors to quant developers in large financial institutions. Unlike more opinionated styles such as Google or GNU, LLVM avoids strong stylistic constraints and focuses instead on clarity and consistency.
This neutrality is exactly why so many projects adopt it as their base style or use it directly without modification. For quant teams working on pricing engines, risk libraries, or low-latency infrastructure, LLVM offers a stable, widely trusted foundation that integrates seamlessly into automated workflows and CI pipelines.
If you need a formatting standard that “just works” across diverse C++ codebases, LLVM is the safest and most broadly compatible choice.
6. Manage Clang Formating in your Codebase
he easiest way to standardize formatting across an entire C++ codebase is to create a .clang-format file at the root of your project. This file acts as the single source of truth for your formatting rules, ensuring every developer, editor, and CI job applies exactly the same style. Once the file is in place, running clang-format becomes fully deterministic: every file in your project will follow the same indentation, spacing, brace placement, and wrapping rules.
A .clang-format file can be as simple as one line—BasedOnStyle: LLVM—or it can define dozens of customized options tailored to your team. Developers don’t need to memorize or manually enforce formatting conventions; the file encodes all rules, and clang-format applies them automatically. Most editors (VSCode, CLion, Vim, Emacs) pick up the configuration instantly, and CI pipelines can run clang-format checks to prevent unformatted code from entering the repository.
An example of .clang-format file:
BasedOnStyle: LLVM
# Indentation & Alignment
IndentWidth: 2
TabWidth: 2
UseTab: Never
# Line Breaking & Wrapping
ColumnLimit: 100
AllowShortIfStatementsOnASingleLine: false
AllowShortFunctionsOnASingleLine: Empty
# Braces & Layout
BreakBeforeBraces: LLVM
BraceWrapping:
AfterNamespace: false
AfterClass: false
AfterControlStatement: false
# Includes
IncludeBlocks: Regroup
SortIncludes: true
# Spacing
SpaceBeforeParens: ControlStatements
SpacesInParentheses: false
SpaceAfterCStyleCast: true
# C++ Specific
Standard: Latest
DerivePointerAlignment: false
PointerAlignment: Left
# Comments
ReflowComments: true
# File Types
DisableFormat: false
Put your file inside your project directory, example of structure:
my-project/
.clang-format
src/
dva.cpp
pricer.cppOnce the .clang-format file is in place:
- No need to specify
-style - No need to pass config flags
- clang-format automatically uses your project’s style rules
Just run:
clang-format -i myfile.cppAnd your team stays fully consistent.
7. Include clang-format in. a pre-commit hook
You might want to do more than that: automate the formatting when commiting to GIT.
For this, create a pre-commit hook file:
.git/hooks/pre-commitMake it executable:
chmod +x .git/hooks/pre-commitPaste this script inside:
#!/bin/bash
# Format only staged C++ files
files=$(git diff --cached --name-only --diff-filter=ACM | grep -E "\.(cpp|hpp|cc|hh|c|h)$")
if [ -z "$files" ]; then
exit 0
fi
echo "Running clang-format on staged C++ files..."
for file in $files; do
clang-format -i "$file"
git add "$file"
done
echo "Clang-format applied."
What it does:
- Detects staged C++ files only
- Runs clang-format using your
.clang-formatrules - Re-adds the formatted files to the commit
- Prevents style drift or “format fixes” later
- Completely automatic
This means a developer cannot commit unformatted C++ code.