What are quantiative developers? In modern finance, the role of the Quantitative Developer (often shortened to Quant Dev) has become essential. Sitting at the intersection of software engineering and quantitative research, quant developers are the bridge between mathematical models and real-world trading systems.
1. What do they do?

A quant developer’s day-to-day work involves:
- Model Implementation: Translating mathematical models into robust C++, Python, or Java code.
- Performance Optimization: Making sure algorithms run within microseconds for low-latency trading or scale to millions of rows in risk simulations.
- Data Engineering: Ingesting, cleaning, and structuring terabytes of market data for model training and backtesting.
- Integration with Systems: Connecting models to execution platforms, risk engines, or reporting pipelines.
- Tooling and Libraries: Writing reusable libraries for derivatives pricing, yield curve construction, Monte Carlo simulation, or time series analysis.
Quant developers need a unique blend of skills:
- Programming Expertise: Strong command of C++ (for performance-critical systems), Python (for prototyping and data analysis), and sometimes Java or Scala.
- Mathematical Understanding: Comfort with linear algebra, probability, statistics, and financial mathematics.
- Financial Knowledge: Understanding of derivatives, risk metrics, pricing conventions, and portfolio management.
- Systems Knowledge: Familiarity with high-performance computing, parallelization, distributed systems, and databases.
2. Who do they work for?
Quantitative developers work across a wide range of financial institutions. In investment banks, they are often responsible for building risk engines and pricing libraries that support traders and risk managers. Hedge funds and proprietary trading firms rely on them to implement high-performance trading strategies and execution algorithms where microseconds matter.
Asset managers employ quant devs to optimize portfolio analytics, factor models, and reporting systems, while insurance companies and corporate treasury departments need their expertise for pricing structured products and managing hedging strategies. Beyond traditional finance, they also play an important role in fintech startups, crypto exchanges, and DeFi platforms, where new forms of trading and risk management require robust technical foundations. Quant developers are also employed by exchanges, clearing houses, regulators, and even central banks, helping to ensure resilient, transparent, and compliant systems. S
ome work in financial software companies and data vendors, creating the analytical libraries used by traders and analysts around the world. Others operate as consultants or freelancers, delivering highly specialized development services for trading desks and quantitative research groups. In every setting, the common thread is the same: they sit at the intersection of mathematics, finance, and software engineering, turning theory into production-ready systems that directly impact how markets function.
3. How much do they make?
Quantitative developers are some of the best-paid engineers in finance, with compensation varying by location, experience, and employer. In London, junior quant devs often start between £70,000 and £90,000, while mid-level developers earn £120,000 to £180,000. Senior positions at investment banks, hedge funds, or proprietary trading firms frequently exceed £200,000, with contractors sometimes billing £700 to £1,200 per day outside IR35. In New York, salaries are even higher: entry-level roles typically fall in the $100,000 to $130,000 range, mid-level developers earn $150,000 to $200,000, and senior hires at top hedge funds can reach $250,000 to $400,000+.
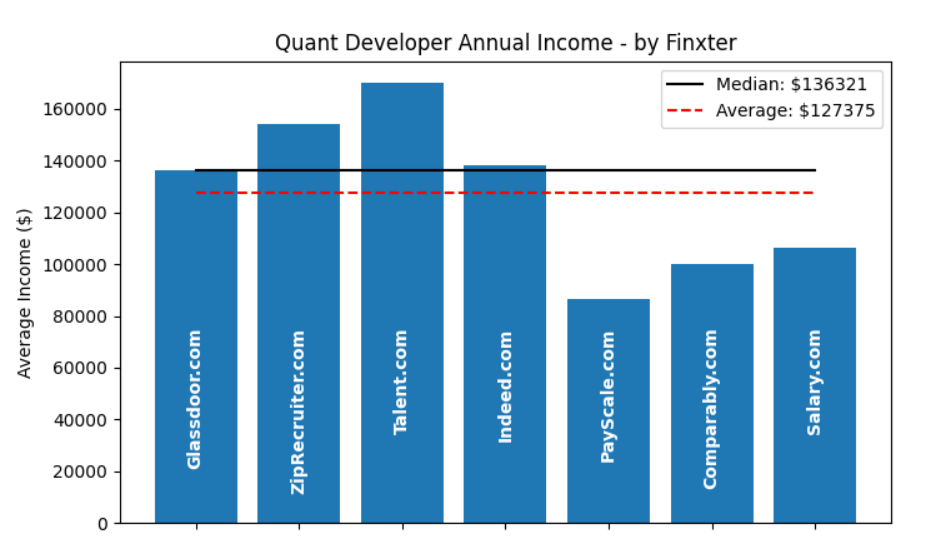
Total compensation is usually boosted by bonuses, which can be very significant in high-performing funds or trading desks. While banks generally offer slightly lower pay in exchange for stability, hedge funds and prop shops provide the highest upside, and fintechs often compete with equity packages instead of cash. Contractors benefit from flexibility and higher daily rates but give up job security and benefits. Within the field, specialization also plays a role: C++ developers working on low-latency trading systems command the strongest salaries, while Python-focused developers, though still well paid, typically earn a bit less. Across regions, U.S. pay tends to outpace European markets, but in every case, quant developers consistently earn well above typical software engineering salaries, reflecting the critical role their work plays in moving global markets.
4. How is the job market for them?
global financial hubs. Investment banks continue to hire them to build and maintain risk engines and pricing platforms, while hedge funds and proprietary trading firms aggressively expand their low-latency trading teams. At the same time, fintech startups and crypto/DeFi firms are creating new demand for developers who can combine finance, data, and engineering skills.
Demand is strongest in cities like London, New York, Hong Kong, and Chicago, with Zurich, Frankfurt, Singapore, and Tokyo also offering strong markets for risk and trading specialists. Employers are especially eager to find C++ developers skilled in performance and latency optimization, while Python developers remain in high demand for data pipelines, prototyping, and machine learning applications.
Experience with distributed systems, cloud platforms, and real-time data processing makes candidates even more competitive. The rise of machine learning in finance has also created hybrid roles that blend software engineering with data science. Job stability tends to be highest at banks, while the biggest upside is offered by hedge funds and prop shops, which often compete fiercely for top candidates by raising salaries.
Contracting opportunities remain strong in London, with high day rates and flexibility, although these roles come with less security. Overall, the market is robust and demand consistently outpaces supply, making skilled quant developers highly valuable in a world where speed, accuracy, and innovation are central to financial success.
5. Conclusion
In conclusion, the role of the quantitative developer has become indispensable in modern finance.
They sit at the intersection of mathematics, software engineering, and financial markets, transforming theory into production-ready systems.
Their work underpins trading platforms, risk engines, pricing libraries, and portfolio analytics.
Without quant developers, many of the models designed by quantitative analysts would remain purely academic.
The profession combines deep technical expertise with financial intuition, a rare and valuable mix.
It is also one of the few roles where C++ mastery continues to provide a strong competitive edge.
At the same time, Python has cemented its place as the language of choice for rapid prototyping and data analysis.
The career offers exceptional compensation, with salaries and day rates far exceeding traditional software roles.
But beyond money, it provides intellectual challenge and direct market impact.
Each line of code written by a quant dev has the potential to influence millions in PnL or mitigate significant risks.
The job market remains strong, with demand outpacing supply across banks, hedge funds, and fintechs.
Global hubs like London, New York, Hong Kong, and Chicago will continue to attract top talent.
Meanwhile, the rise of machine learning, cloud computing, and decentralized finance is expanding the scope of opportunities.
Quant developers are no longer confined to traditional institutions—they are shaping the future of fintech and digital assets.
Those who excel combine low-level performance engineering with an ability to adapt to new paradigms.
The best quant devs are lifelong learners, constantly updating their skills in algorithms, systems, and finance.
For aspiring professionals, it is a career that rewards curiosity, rigor, and resilience.
For the industry, it is a role that ensures innovation and stability in equal measure.
Ultimately, quantitative developers are the engineers behind modern markets, ensuring that complex ideas can operate at scale.
Their contribution is both foundational and forward-looking, making them central to the evolution of global finance.